brinla
INLA Split Plot Model example
Julian Faraway 22 September 2020
See the introduction for an overview. Load the libraries:
library(ggplot2)
library(INLA)
Data
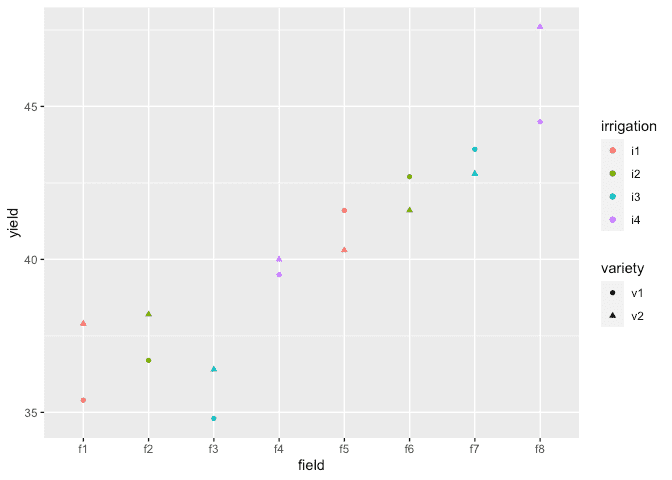
Load in and plot the data:
data(irrigation, package="faraway")
summary(irrigation)
field irrigation variety yield
f1 :2 i1:4 v1:8 Min. :34.8
f2 :2 i2:4 v2:8 1st Qu.:37.6
f3 :2 i3:4 Median :40.1
f4 :2 i4:4 Mean :40.2
f5 :2 3rd Qu.:42.7
f6 :2 Max. :47.6
(Other):4
ggplot(irrigation, aes(y=yield, x=field, shape=variety, color=irrigation)) + geom_point()
Default INLA fit
formula <- yield ~ irrigation + variety +f(field, model="iid")
result <- inla(formula, family="gaussian", data=irrigation)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = irrigation)"
Time used:
Pre = 1.34, Running = 0.141, Post = 0.0792, Total = 1.56
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 38.469 2.810 32.829 38.461 44.151 38.452 0
irrigationi2 0.949 3.949 -7.047 0.957 8.876 0.969 0
irrigationi3 0.552 3.949 -7.442 0.560 8.481 0.571 0
irrigationi4 4.024 3.949 -3.986 4.037 11.939 4.054 0
varietyv2 0.750 0.618 -0.491 0.750 1.989 0.750 0
Random effects:
Name Model
field IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 0.867 0.428 0.224 0.802 1.875 0.672
Precision for field 0.105 0.076 0.020 0.088 0.288 0.061
Expected number of effective parameters(stdev): 8.71(0.29)
Number of equivalent replicates : 1.84
Marginal log-Likelihood: -66.93
Default looks more plausible than one way and RBD examples.
Compute the transforms to an SD scale for the field and error. Make a table of summary statistics for the posteriors:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab=sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaepsilon,silent=TRUE))
colnames(restab) = c("mu","ir2","ir3","ir4","v2","alpha","epsilon")
data.frame(restab)
mu ir2 ir3 ir4 v2 alpha epsilon
mean 38.469 0.94858 0.55178 4.0238 0.74971 3.6514 1.191
sd 2.8106 3.9501 3.9501 3.9503 0.61835 1.3537 0.3602
quant0.025 32.823 -7.0565 -7.4515 -3.9959 -0.49254 1.8567 0.73092
quant0.25 36.772 -1.4166 -1.8137 1.6614 0.36647 2.7362 0.94892
quant0.5 38.447 0.93806 0.54067 4.0178 0.74668 3.3724 1.1156
quant0.75 40.129 3.2859 2.8887 6.364 1.1269 4.2396 1.3409
quant0.975 44.136 8.8579 8.4629 11.919 1.9856 7.0837 2.1047
Also construct a plot the SD posteriors:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,nrow(sigmaalpha),labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("yield")+ylab("density")+xlim(0,10)
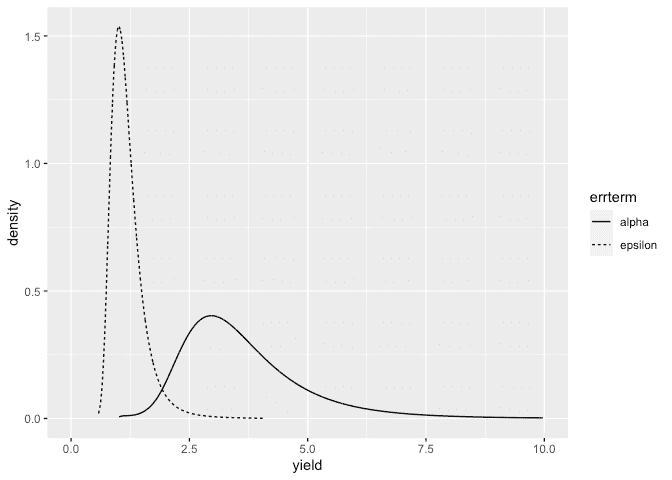
Posteriors look OK.
Informative Gamma priors on the precisions
Now try more informative gamma priors for the precisions. Define it so
the mean value of gamma prior is set to the inverse of the variance of
the residuals of the fixed-effects only model. We expect the two error
variances to be lower than this variance so this is an overestimate. The
variance of the gamma prior (for the precision) is controlled by the
apar shape parameter.
apar <- 0.5
lmod <- lm(yield ~ irrigation+variety, data=irrigation)
bpar <- apar*var(residuals(lmod))
lgprior <- list(prec = list(prior="loggamma", param = c(apar,bpar)))
formula = yield ~ irrigation+variety+f(field, model="iid", hyper = lgprior)
result <- inla(formula, family="gaussian", data=irrigation)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = irrigation)"
Time used:
Pre = 1.32, Running = 0.153, Post = 0.0842, Total = 1.56
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 38.491 3.440 31.569 38.477 45.489 38.462 0
irrigationi2 0.924 4.844 -8.936 0.939 10.674 0.958 0
irrigationi3 0.529 4.844 -9.328 0.542 10.281 0.560 0
irrigationi4 3.986 4.845 -5.899 4.009 13.713 4.037 0
varietyv2 0.750 0.605 -0.463 0.750 1.961 0.750 0
Random effects:
Name Model
field IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 0.892 0.425 0.260 0.826 1.896 0.692
Precision for field 0.070 0.047 0.012 0.059 0.188 0.039
Expected number of effective parameters(stdev): 8.80(0.193)
Number of equivalent replicates : 1.82
Marginal log-Likelihood: -55.86
Compute the summaries as before:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab=sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaepsilon,silent=TRUE))
colnames(restab) = c("mu","ir2","ir3","ir4","v2","alpha","epsilon")
data.frame(restab)
mu ir2 ir3 ir4 v2 alpha epsilon
mean 38.491 0.92369 0.52856 3.9859 0.74973 4.5237 1.1611
sd 3.4413 4.8459 4.8459 4.8464 0.60482 1.8183 0.31715
quant0.025 31.561 -8.9479 -9.3396 -5.9123 -0.46439 2.3073 0.72703
quant0.25 36.456 -1.9131 -2.3089 1.154 0.3723 3.3008 0.93973
quant0.5 38.46 0.91484 0.51868 3.9851 0.74676 4.1029 1.0997
quant0.75 40.474 3.7313 3.3355 6.7988 1.1212 5.2456 1.3111
quant0.975 45.469 10.65 10.258 13.688 1.9576 9.2349 1.9532
Make the plots:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,nrow(sigmaalpha),labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("yield")+ylab("density")+xlim(0,10)
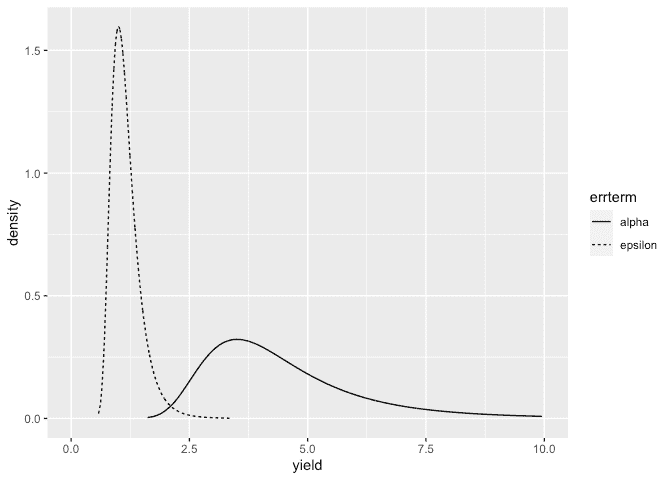
Posteriors look OK.
Penalized Complexity Prior
In Simpson et al (2015), penalized complexity priors are proposed. This requires that we specify a scaling for the SDs of the random effects. We use the SD of the residuals of the fixed effects only model (what might be called the base model in the paper) to provide this scaling.
lmod <- lm(yield ~ irrigation+variety, irrigation)
sdres <- sd(residuals(lmod))
pcprior <- list(prec = list(prior="pc.prec", param = c(3*sdres,0.01)))
formula <- yield ~ irrigation+variety+f(field, model="iid", hyper = pcprior)
result <- inla(formula, family="gaussian", data=irrigation)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = irrigation)"
Time used:
Pre = 1.32, Running = 0.145, Post = 0.0828, Total = 1.55
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 38.477 3.042 32.361 38.469 44.639 38.457 0
irrigationi2 0.940 4.280 -7.731 0.949 9.549 0.962 0
irrigationi3 0.544 4.280 -8.125 0.552 9.154 0.565 0
irrigationi4 4.011 4.281 -4.674 4.025 12.604 4.045 0
varietyv2 0.750 0.606 -0.467 0.750 1.964 0.750 0
Random effects:
Name Model
field IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 0.886 0.425 0.253 0.82 1.891 0.686
Precision for field 0.082 0.053 0.018 0.07 0.214 0.049
Expected number of effective parameters(stdev): 8.77(0.215)
Number of equivalent replicates : 1.82
Marginal log-Likelihood: -56.40
Compute the summaries as before:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab=sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab=cbind(restab, inla.zmarginal(sigmaepsilon,silent=TRUE))
colnames(restab) = c("mu","ir2","ir3","ir4","v2","alpha","epsilon")
data.frame(restab)
mu ir2 ir3 ir4 v2 alpha epsilon
mean 38.477 0.93976 0.54353 4.0106 0.74972 4.0372 1.1676
sd 3.0424 4.2806 4.2806 4.2808 0.60614 1.3393 0.32498
quant0.025 32.355 -7.7417 -8.1361 -4.6858 -0.46761 2.1601 0.72807
quant0.25 36.614 -1.6624 -2.059 1.4111 0.37106 3.0892 0.94212
quant0.5 38.454 0.92811 0.53126 4.0037 0.74674 3.7841 1.1037
quant0.75 40.3 3.5109 3.1143 6.5847 1.1224 4.7019 1.3181
quant0.975 44.617 9.5218 9.1274 12.579 1.9608 7.3651 1.9816
Make the plots:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,nrow(sigmaalpha),labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("yield")+ylab("density")+xlim(0,10)
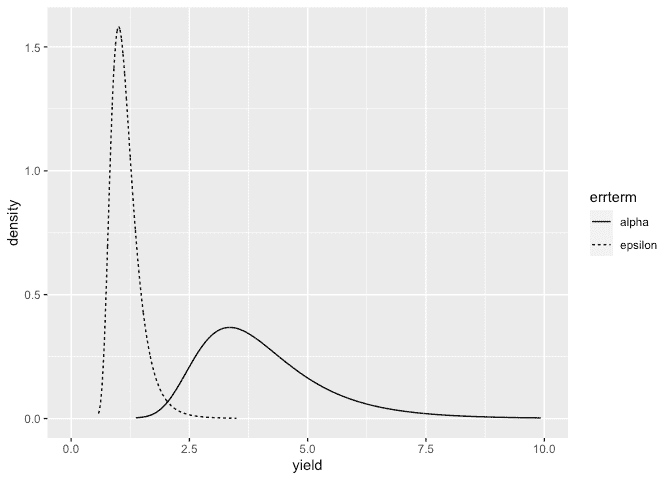
Posteriors look OK.
Package version info
sessionInfo()
R version 4.0.2 (2020-06-22)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods base
other attached packages:
[1] INLA_20.03.17 foreach_1.5.0 sp_1.4-2 Matrix_1.2-18 ggplot2_3.3.2 knitr_1.29
loaded via a namespace (and not attached):
[1] pillar_1.4.6 compiler_4.0.2 iterators_1.0.12 tools_4.0.2 digest_0.6.25
[6] evaluate_0.14 lifecycle_0.2.0 tibble_3.0.3 gtable_0.3.0 lattice_0.20-41
[11] pkgconfig_2.0.3 rlang_0.4.7 yaml_2.2.1 xfun_0.16 withr_2.2.0
[16] dplyr_1.0.2 stringr_1.4.0 MatrixModels_0.4-1 generics_0.0.2 vctrs_0.3.4
[21] grid_4.0.2 tidyselect_1.1.0 glue_1.4.2 R6_2.4.1 rmarkdown_2.3
[26] farver_2.0.3 purrr_0.3.4 magrittr_1.5 splines_4.0.2 scales_1.1.1
[31] codetools_0.2-16 ellipsis_0.3.1 htmltools_0.5.0.9000 colorspace_1.4-1 Deriv_4.0.1
[36] labeling_0.3 stringi_1.4.6 munsell_0.5.0 crayon_1.3.4