brinla
INLA for One Way Anova with a random effect
Julian Faraway 22 September 2020
See the introduction for an overview. Load the libraries:
library(ggplot2)
library(INLA)
Data
Load up and look at the data:
data(pulp, package="faraway")
summary(pulp)
bright operator
Min. :59.8 a:5
1st Qu.:60.0 b:5
Median :60.5 c:5
Mean :60.4 d:5
3rd Qu.:60.7
Max. :61.0
ggplot(pulp, aes(x=operator, y=bright))+geom_point(position = position_jitter(width=0.1, height=0.0))
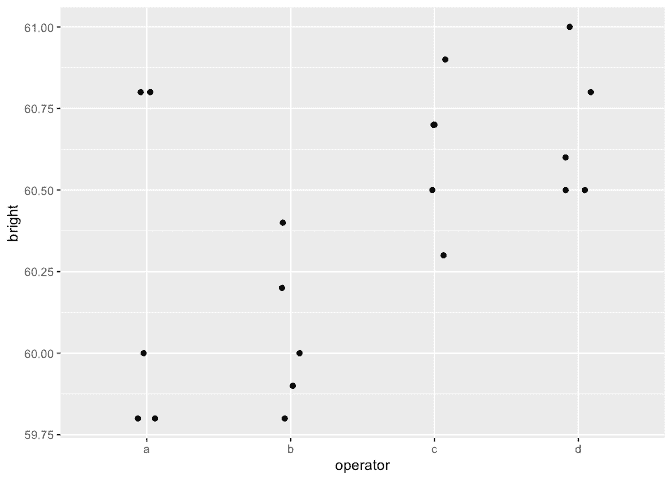
Default fit
Run the default INLA model:
formula <- bright ~ f(operator, model="iid")
result <- inla(formula, family="gaussian", data=pulp)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = pulp)"
Time used:
Pre = 0.976, Running = 0.134, Post = 0.0733, Total = 1.18
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 60.4 0.093 60.216 60.4 60.584 60.4 0
Random effects:
Name Model
operator IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 7.04 2.25 3.41 6.78 12.13 6.30
Precision for operator 19120.58 20029.37 100.47 12920.98 73424.29 14.40
Expected number of effective parameters(stdev): 1.17(0.488)
Number of equivalent replicates : 17.09
Marginal log-Likelihood: -19.41
Precision for the operator term is unreasonably high. This is due to the diffuse gamma prior on the precisions. Problems are seen with other packages also. We can improve the calculation but result would remain implausible so it is better we change the prior.
Informative but weak prior on the SDs
Try a truncated normal prior with low precision instead. A precision of 0.01 corresponds to an SD of 10. This is substantially larger than the SD of the response so the information supplied is very weak.
tnprior <- list(prec = list(prior="logtnormal", param = c(0,0.01)))
formula <- bright ~ f(operator, model="iid", hyper = tnprior)
result <- inla(formula, family="gaussian", data=pulp)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = pulp)"
Time used:
Pre = 1.01, Running = 0.146, Post = 0.0748, Total = 1.23
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 60.4 0.41 59.612 60.4 61.188 60.4 0.022
Random effects:
Name Model
operator IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 10.44 3.52e+00 4.728 10.04 18.40 9.236
Precision for operator 68999.86 4.94e+07 0.231 6.67 139.05 0.176
Expected number of effective parameters(stdev): 3.43(0.637)
Number of equivalent replicates : 5.83
Marginal log-Likelihood: -20.36
The results appear more plausible. Transform to the SD scale. Make a table of summary statistics for the posteriors:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab <- sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaepsilon,silent = TRUE))
restab <- cbind(restab, sapply(result$marginals.random$operator,function(x) inla.zmarginal(x, silent = TRUE)))
colnames(restab) <- c("mu","alpha","epsilon",levels(pulp$operator))
data.frame(restab)
mu alpha epsilon a b c d
mean 60.4 0.5489 0.32346 -0.1298 -0.27684 0.17976 0.2274
sd 0.41052 0.59606 0.057735 0.42072 0.42591 0.42327 0.42414
quant0.025 59.608 0.082628 0.23336 -0.96363 -1.141 -0.59516 -0.53446
quant0.25 60.255 0.24926 0.28217 -0.28764 -0.44163 0.0076432 0.045395
quant0.5 60.398 0.38448 0.31548 -0.11579 -0.25576 0.15884 0.20378
quant0.75 60.54 0.6217 0.35584 0.029438 -0.092496 0.3353 0.38524
quant0.975 61.187 2.051 0.45891 0.64599 0.47118 1.0208 1.0773
The results are now comparable to previous fits to this data using likelihood and MCMC-based methods. Plot the posterior densities for the two SD terms:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,dim(sigmaalpha)[1],labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("bright")+ylab("density")+xlim(0,2)
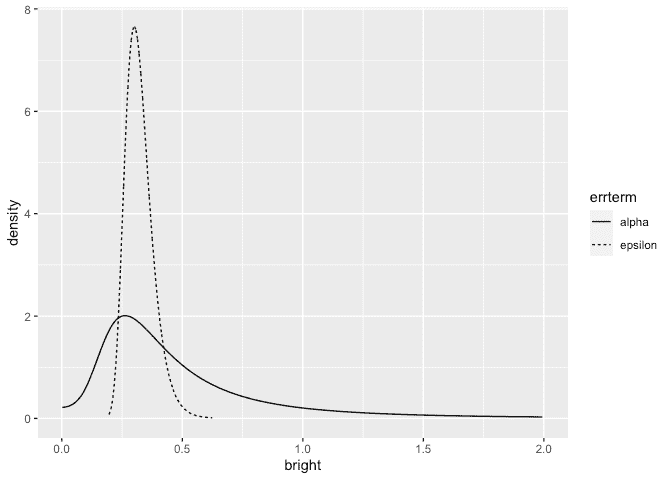
We see that the operator SD less precisely known than the error SD.
We can compute the probability that the operator SD is smaller than 0.1:
inla.pmarginal(0.1, sigmaalpha)
[1] 0.034449
The probability is small but not negligible.
Informative gamma priors on the precisions
Now try more informative gamma priors for the precisions. Define it so
the mean value of gamma prior is set to the inverse of the variance of
the response. We expect the two error variances to be lower than the
response variance so this is an overestimate. The variance of the gamma
prior (for the precision) is controlled by the apar shape parameter in
the code. apar=1 is the exponential distribution. Shape values less
than one result in densities that have a mode at zero and decrease
monotonely. These have greater variance and hence less informative.
apar <- 0.5
bpar <- var(pulp$bright)*apar
lgprior <- list(prec = list(prior="loggamma", param = c(apar,bpar)))
formula <- bright ~ f(operator, model="iid", hyper = lgprior)
result <- inla(formula, family="gaussian", data=pulp)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = pulp)"
Time used:
Pre = 0.949, Running = 0.131, Post = 0.0766, Total = 1.16
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 60.4 0.233 59.931 60.4 60.869 60.4 0.002
Random effects:
Name Model
operator IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 10.59 3.52 4.87 10.20 18.53 9.41
Precision for operator 11.12 9.02 1.17 8.74 35.00 4.53
Expected number of effective parameters(stdev): 3.49(0.364)
Number of equivalent replicates : 5.73
Marginal log-Likelihood: -17.93
Compute the summaries as before:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab <- sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaepsilon,silent = TRUE))
restab <- cbind(restab, sapply(result$marginals.random$operator,function(x) inla.zmarginal(x, silent = TRUE)))
colnames(restab) <- c("mu","alpha","epsilon",levels(pulp$operator))
data.frame(restab)
mu alpha epsilon a b c d
mean 60.4 0.38937 0.32063 -0.13278 -0.28218 0.18258 0.23238
sd 0.23275 0.20389 0.056154 0.24942 0.25188 0.25004 0.25086
quant0.025 59.93 0.16902 0.23255 -0.64645 -0.81221 -0.30165 -0.24821
quant0.25 60.271 0.25984 0.28052 -0.27426 -0.42425 0.034853 0.08279
quant0.5 60.399 0.33765 0.31303 -0.12944 -0.27424 0.17508 0.22334
quant0.75 60.527 0.45472 0.35221 0.010768 -0.13309 0.32149 0.37148
quant0.975 60.868 0.92011 0.45204 0.35291 0.19263 0.69904 0.75429
Make the plots:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,dim(sigmaalpha)[1],labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("bright")+ylab("density")+xlim(0,2)
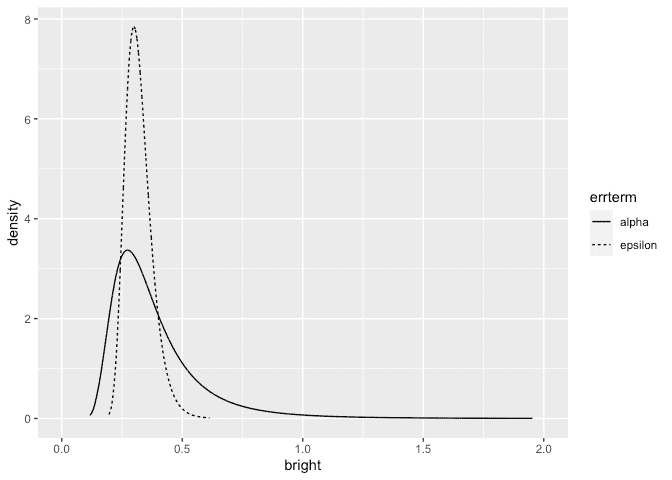
The posterior for the error SD is quite similar to that seen previously but the operator SD is larger and bounded away from zero.
We can compute the probability that the operator SD is smaller than 0.1:
inla.pmarginal(0.1, sigmaalpha)
[1] 7.2871e-05
The probability is very small. The choice of prior may be unsuitable in that no density is placed on an SD=0 (or infinite precision). We also have very little prior weight on low SD/high precision values. This leads to a posterior for the operator with very little density assigned to small values of the SD. But we can see from looking at the data or from prior analyses of the data that there is some possibility that the operator SD is negligibly small.
Penalized Complexity Prior
In Simpson et al (2015), penalized complexity priors are proposed. This requires that we specify a scaling for the SDs of the random effects. We use the SD of the residuals of the fixed effects only model (what might be called the base model in the paper) to provide this scaling.
sdres <- sd(pulp$bright)
pcprior <- list(prec = list(prior="pc.prec", param = c(3*sdres,0.01)))
formula <- bright ~ f(operator, model="iid", hyper = pcprior)
result <- inla(formula, family="gaussian", data=pulp)
result <- inla.hyperpar(result)
summary(result)
Call:
"inla(formula = formula, family = \"gaussian\", data = pulp)"
Time used:
Pre = 0.949, Running = 0.152, Post = 0.0778, Total = 1.18
Fixed effects:
mean sd 0.025quant 0.5quant 0.975quant mode kld
(Intercept) 60.4 0.173 60.049 60.4 60.752 60.4 0
Random effects:
Name Model
operator IID model
Model hyperparameters:
mean sd 0.025quant 0.5quant 0.975quant mode
Precision for the Gaussian observations 10.09 3.51e+00 4.48 9.67 18.05 8.82
Precision for operator 954240.12 6.54e+08 2.24 16.61 1101.86 5.90
Expected number of effective parameters(stdev): 3.03(0.742)
Number of equivalent replicates : 6.61
Marginal log-Likelihood: -17.97
Compute the summaries as before:
sigmaalpha <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[2]])
sigmaepsilon <- inla.tmarginal(function(x) 1/sqrt(exp(x)),result$internal.marginals.hyperpar[[1]])
restab <- sapply(result$marginals.fixed, function(x) inla.zmarginal(x,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaalpha,silent=TRUE))
restab <- cbind(restab, inla.zmarginal(sigmaepsilon,silent = TRUE))
restab <- cbind(restab, sapply(result$marginals.random$operator,function(x) inla.zmarginal(x, silent = TRUE)))
colnames(restab) <- c("mu","alpha","epsilon",levels(pulp$operator))
data.frame(restab)
mu alpha epsilon a b c d
mean 60.4 0.27121 0.32985 -0.10938 -0.23306 0.15018 0.19075
sd 0.17283 0.15847 0.06051 0.19093 0.20358 0.19416 0.19867
quant0.025 60.048 0.030079 0.23563 -0.52204 -0.67978 -0.20284 -0.15633
quant0.25 60.302 0.16472 0.2864 -0.21783 -0.35386 0.024033 0.055881
quant0.5 60.399 0.24505 0.32141 -0.096252 -0.21757 0.13326 0.17326
quant0.75 60.496 0.34735 0.36398 0.0044809 -0.094222 0.26019 0.3052
quant0.975 60.75 0.66253 0.47167 0.24942 0.11059 0.57213 0.62442
Make the plots:
ddf <- data.frame(rbind(sigmaalpha,sigmaepsilon),errterm=gl(2,dim(sigmaalpha)[1],labels = c("alpha","epsilon")))
ggplot(ddf, aes(x,y, linetype=errterm))+geom_line()+xlab("bright")+ylab("density")+xlim(0,2)
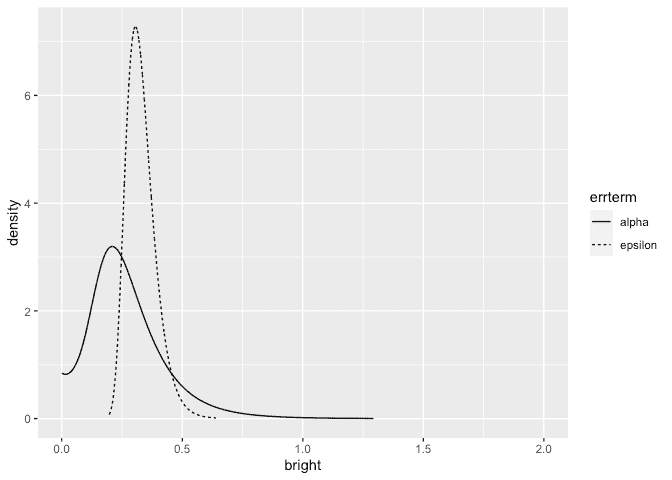
We get a similar result to the truncated normal prior used earlier although the operator SD is generally smaller.
We can compute the probability that the operator SD is smaller than 0.1:
inla.pmarginal(0.1, sigmaalpha)
[1] 0.10372
The probability is small but not insubstantial.
Package version info
sessionInfo()
R version 4.0.2 (2020-06-22)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods base
other attached packages:
[1] INLA_20.03.17 foreach_1.5.0 sp_1.4-2 Matrix_1.2-18 ggplot2_3.3.2 knitr_1.29
loaded via a namespace (and not attached):
[1] pillar_1.4.6 compiler_4.0.2 iterators_1.0.12 tools_4.0.2 digest_0.6.25
[6] evaluate_0.14 lifecycle_0.2.0 tibble_3.0.3 gtable_0.3.0 lattice_0.20-41
[11] pkgconfig_2.0.3 rlang_0.4.7 yaml_2.2.1 xfun_0.16 withr_2.2.0
[16] dplyr_1.0.2 stringr_1.4.0 MatrixModels_0.4-1 generics_0.0.2 vctrs_0.3.4
[21] grid_4.0.2 tidyselect_1.1.0 glue_1.4.2 R6_2.4.1 rmarkdown_2.3
[26] farver_2.0.3 purrr_0.3.4 magrittr_1.5 splines_4.0.2 scales_1.1.1
[31] codetools_0.2-16 ellipsis_0.3.1 htmltools_0.5.0.9000 colorspace_1.4-1 Deriv_4.0.1
[36] labeling_0.3 stringi_1.4.6 munsell_0.5.0 crayon_1.3.4